| ENG RUS | Timus Online Judge |
1122. GameTime limit: 1.0 second Memory limit: 64 MB At SKB Kontur we have to work much.
So there is no sin in taking a rest and playing from time to time.
Consider for example the following famous one-player game. 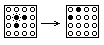 We have a 4×4 field. There are chips with one side painted white and another side painted black on the field. Some of the chips are with their white side up and the others are with their white side down at the moment. Each move consists in turning over a chip together with all the chips that are adjacent to it vertically and horizontally (i.e. 5 chips altogether).
The aim is to come to the position in which all the chips are with the same side up. 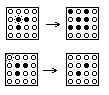 Naturally, one is easily bored with this game
because interesting and unexpected positions become fewer as time goes on.
That is why a modified version of the game is now more popular at SKB Kontur.
In this version a move consists in turning over a fixed combination of chips
within a 3×3 square. For example, a move may consist in turning over all
the diagonal neighbors of a chosen chip.  The combination of chips is chosen arbitrarily; it may be assigned in the form of a 3×3 field in which the central cell corresponds to the cell at which a move as made. For example, in picture at the left the upper combination corresponds to a standard game and the lower combination is for the game described in the previous paragraph. Note that a combination can be asymmetrical. Each move is made at one of the cells of the playing field (i.e. the central cell of the 3×3 move-defining square is selected among the field's cells). Prescriptions to turn over chips at cells which are outside the 4×4 field are ignored. In this game it would be nice to know if it is possible to reach a position in which all the chips are with the same side up and if it's possible to do this then in how many moves. You are to write a program which answers these questions. InputThe first four lines describe the initial arrangement of chips.
A symbol "W" stands for a chip which lies with its white side up
and a symbol "B" stands for a chip which lies with its black side up.
The next three lines describe a move: the chips that are to be turned over
are shown by "1" and others are shown by "0". OutputIf it is impossible to reach the aim of the game you should output
the word "Impossible", otherwise you should output the minimal number
of moves necessary to come to the final position. Sample
Problem Author: Leonid Volkov, Oleg Kats, Alexander Somov Problem Source: USU Open Collegiate Programming Contest October'2001 Junior Session Tags: game |
