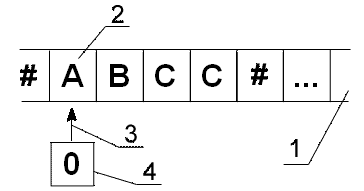Машина Тьюринга используется для исследований вычислимости и хорошо знакома людям, занимающимся теорией алгоритмов. Дадим краткое описание этой абстракции. Машина Тьюринга — автоматическое устройство, которое работает с лентой (1) потенциально неограниченной длины. Лента разделена на ячейки, каждая из которых хранит один символ. Одна из ячеек называется текущей (2). В любой момент времени машина Тьюринга находится в некотором состоянии, которое записано в управляющем устройстве (4). Кроме того, головка чтения/записи (3) управляющего устройства указывает на текущую ячейку.

Управляющее устройство выполняет одно действие за единицу времени (шаг). Действие включает возможное изменение состояния, возможное изменение символа в текущей ячейке и возможное движение головки чтения/записи в соседнюю ячейку. Эти действия определены в специальной таблице, называемой управляющей таблицей. Обозначим движение вдоль ленты следующими символами: "<" — влево, ">" — вправо, "=" — движение отсутствует.

Управляющая таблица является программой для машины Тьюринга. Работа машины Тьюринга считается завершённой, когда ни одна строка управляющей таблицы не содержит комбинации текущего символа и текущего состояния.

Текущее состояние	Текущий символ	Новое состояние	Новый символ	Движение
1	-	2	-	>
2	-	3	+	>
3	#	4	#	<
4	+	4	+	<
4	-	5	-	=

Замечание. Этот пример только иллюстрирует определение таблицы.

Исходные данные для машины Тьюринга заранее помещаются в клетки ленты. Результат записывается на ту же ленту. Будем считать, что исходное состояние машины Тьюринга равно 1, а входные данные на ленте ограничены символами '#' с обоих концов. (Все ячейки ленты, кроме заполненных минусами, заполнены символами '#'.) Головка управляющего устройства указывает на самый левый символ '−' входных данных. В начале работы лента содержит знак '−' (минус), повторённый n раз (1 ≤ n ≤ 200), а ввод вашей программы содержит целое число k.

Представьте, что минусы расположены по кругу. Начиная с первого, каждый k-й незачёркнутый минус зачёркивается, то есть превращается в '+' (плюс). Исполнение останавливается, когда остаётся только один незачёркнутый минус. Ваша задача — описать управляющую таблицу для машины Тьюринга, которая зачеркнёт все минусы, кроме одного (его позиция определена в соответствии с описанным выше алгоритмом, но вы можете использовать любой способ нахождения позиции) для заданного k. Например, для n = 10 и k = 3 четвёртый минус останется незачёркнутым.

Разрешается записывать на ленту следующие символы: '+', '#', 'A'..'Z'. Клетки, изначально заполненные минусами, могут содержать только символы '−' и '+'. Клетка, в которой останется минус, не должна меняться. После выполнения головка чтения/записи должна указывать на незачёркнутый минус. Количество шагов s не должно превосходить 1 000 000. Количество строк p в таблице управления не должно превосходить 10 000. Размер ленты ограничен 10 001 ячейкой (5000 с каждой стороны от начального положения головки чтения/записи).

Ввод содержит целое число k (1 ≤ k ≤ 200).

Вывод описывает управляющую таблицу машины Тьюринга для заданного значения k. Первая строка вывода содержит число строк p таблицы (1 < p < 10 000). Затем следует p строк, описывающих саму таблицу. Каждая строка таблицы содержит пять элементов: текущее состояние (целое число), текущий символ (символ), новое состояние (целое число), новый символ (символ), направление движения (символ). Элементы строки разделены одиночными пробелами. Номера состояний могут быть от 1 до 30 000.

Обратите внимание, что этот пример правилен только для n = 2. Он только показывает формат вывода.