| ENG RUS | Timus Online Judge |
УрКОП 2020
Соревнование завершено
H. Полёт на ядреОграничение времени: 2.0 секунды Ограничение памяти: 256 МБ Барон Мюнхгаузен участвует в очередной баталии, которая происходит на плоскости с
прямоугольной декартовой системой координат. Командир приказал ему как можно быстрее попасть в центр координат. Дело за малым — нужно сесть на ядро и спрыгнуть с него как можно ближе к цели. На поле есть n пушечных батарей, и Мюнхгаузен находится в одной из них. Батареи можно считать точками, i-я батарея имеет координаты (xi, yi). Находясь в одной из батарей, барон может выстрелить в сторону любой другой батареи и сесть на ядро; стрелять мимо батареи нельзя — это подорвёт авторитет барона. Ядро не останавливается, достигнув батареи, а продолжает лететь бесконечно далеко. Пролетая над любой из батарей, Мюнхгаузен может спрыгнуть с ядра; после этого он снова сможет выстрелить в сторону другой батареи. Таким образом барон может свободно перемещаться между батареями. Когда барон решит, что он близок к центру координат, он спрыгнет с ядра и дальше пойдёт пешком. Определите наименьшее расстояние, на которое барон Мюнхгаузен может приблизиться к центру координат, перемещаясь только на ядрах. Исходные данныеВ первой строке задано целое число n (2 ≤ n ≤ 105) — количество батарей. В следующих n строках заданы целые числа xi и yi, разделённые пробелом (−105 ≤ xi, yi ≤ 105) — координаты очередной батареи. Гарантируется, что не существует двух батарей с совпадающими координатами. РезультатВыведите одно действительное число — наименьшее расстояние, на которое барон Мюнхгаузен может приблизиться к центру координат, перемещаясь только на ядрах. Ваш ответ считается правильным, если абсолютная или относительная его погрешность не превышает 10−6. Примеры
ЗамечанияИллюстрация ко второму примеру: 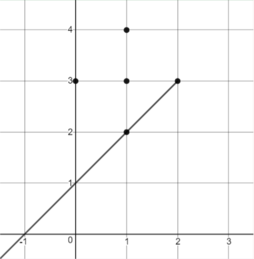 Автор задачи: Валентин Зуев Источник задачи: Уральская командная олимпиада по программированию 2020 |
