| ENG RUS | Timus Online Judge |
Чемпионат Урала 2005 Тур I
Соревнование завершено
G. Пирамида декана 2Ограничение времени: 1.0 секунды Ограничение памяти: 64 МБ На Чемпионате Урала-2004 была задача о пирамиде декана. Вкратце ее содержание таково:
На столе декана матмеха УрГУ стоит прозрачная пирамида, формой напоминающая египетские. Живущая на матмехе легенда гласит, что при отчислении неуспевающих студентов декан дает двоечникам последний шанс. Он кладет неподписанный приказ об отчислении на один край стола и ставит пирамиду на другой край. Если студент сможет, использовав не более 70 перекатываний пирамиды, закрыть ей место предполагаемой подписи декана, то в последний раз он остается на факультете. В задаче требовалось определить, как близко можно подкатить пирамиду декана к заданной точке при условии, что ее боковые грани являются равностронними треугольниками, и если пирамида перекатывалась на свое основание через какое-то ребро, то следующим шагом ее можно перекатывать только через противоположное ребро. После чемпионата Урала 2004 года по рядам двоечников матмеха пронесся вздох облегчения, они узнали секретные свойства пирамиды Магаза Оразкимовича и простейший алгоритм определения возможных точек нахождения пирамиды на столе. Запомнить этот алгоритм было гораздо легче, чем
добросовестно учиться и они уже считали себя спасенными. Лишь одно сомнение терзало их души: не перепутали ли чего авторы той задачи? Съемки пирамиды скрытой камерой с разных ракурсов и последующее обращение со снимками к отличникам матмеха позволили узнать печальную истину: грани пирамиды НЕ ЯВЛЯЛИСЬ равносторонними треугольниками, как они надеялись, а были всего лишь равнобедренными! Да и странное ограничение на перекатывание через квадратное основание тоже вполне могло оказаться выдумкой авторов задачи. Горе двоечникам, горе! Ведь хотя это и легенда, но она может иметь под собой реальные основания, и пирамида на столе декана действительно стоит... Помогите же им в последний раз. Выясните, как лучше
подкатывать пирамиду к точке подписи. Вам сообщат число N — максимальное число перекатываний,
которое разрешает декан. Будут даны точные размеры пирамиды (длина
ребра основания A1 и длина бокового ребра A2) в сантиметрах. На глаз можно сказать, что отношение A2/A1 лежит в пределах от 0.9 до 1.9. Считается, что декан достаточно строг и кладет приказ далеко от пирамиды, поэтому можете считать, что расстояние от исходного расположения пирамиды до желаемой точки не менее 20.05 * A1.
Будем считать, что в начальный момент времени пирамида стоит на своем основании, ребра основания параллельны осям координат, центр основания находится в точке (0,0). Вы должны найти последовательность перекатываний,
которая переводит пирамиду как можно ближе к точке (X,Y). На последнем шаге пирамида также должна стоять на своем основании, ребра основания могут быть ориентированы как угодно, но расстояние между центром основания и точкой (X,Y) должно быть как можно меньше. При прочих равных условиях минимизируйте число перекатываний. Разрешается использовать менее N перекатываний. Перекатывать можно с любой грани на другую только через общее ребро, и только так, чтобы в процессе перекатывания это ребро
не смещалось по поверхности стола. Исходные данныеДаны числа A1 и A2 (в сантиметрах, оба лежат в интервале от 0.1 до 10), далее числа X и Y — координаты той самой заветной точки подписи на лежащем на столе приказе. Последним идёт число N (2 ≤ N ≤ 32).
РезультатФормат вывода такой. Сначала выведите получившееся у Вас расстояние (в сантиметрах с точностью 3 знака после десятичной точки) между конечным расположением центра основания пирамиды и точкой подписи. Потом выведите число потребовавшихся вам перекатываний M (0 ≤ M ≤ N).
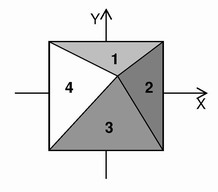 В следующей строке перечислите список из M+1 номеров граней, на которых будет находиться пирамида при перекатывании. Используйте пробел для разделения чисел в списке. Не забудьте в начале этого списка вывести номер основания пирамиды, на котором она стоит в начальный момент времени.
Нумерация граней следующая: основание — 0; боковые грани нумеруются числами 1, 2, 3 и 4 по часовой стрелке при взгляде сверху; боковая грань, смотрящая в положительном направлении оси OY имеет номер 1.
Пример
Автор задачи: Александр Мироненко Источник задачи: IX Чемпионат Урала по программированию. Екатеринбург, УрГУ, 19-24 апреля 2005г. |
