| ENG RUS | Timus Online Judge |
Соревнование школьников. Октябрь 2004
Соревнование завершено
G. Джинн-бомбардировки 2Ограничение времени: 1.0 секунды Ограничение памяти: 64 МБ Во многом благодаря вашей работе над джинн-бомбардировками они успешно прошли испытания. Но Модесту Матвеевичу Камноедову осталось решить еще несколько задач, связанных с увеличением их эффективности. Самой простой из них является нахождение площади поражения джинн-бомбардировки. Будем предполагать, что джинн-бомбардировке подвергается квадратный участок плоскости, задаваемый неравенствами 0 ≤ x ≤ 1, 0 ≤ y ≤ 1. Область поражения одной джинн-бомбы – это круг с центром в точке падения. Точка плоскости считается пораженной, если она попала в область поражения хотя бы одной джинн-бомбы. Мы называем процентом поражения отношение площади пораженной зоны к общей площади. Ваша задача - найти процент поражения. 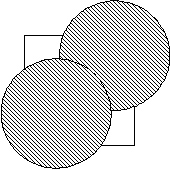 Исходные данныеВ первой строчке находится число N – число сброшенных джинн-бомб (N ≤ 10). В следующих N строках находятся по три действительных числа x, y, r – координаты точки падения джинн-бомбы и радиус её поражения (0 ≤ x, y, r ≤ 1). РезультатНа выход должно подаваться единственное действительное число – процент поражения квадрата задаваемого неравенствами 0 ≤ x ≤ 1, 0 ≤ y ≤ 1. Ответ должен быть дан с точностью не меньшей одного процента. Примеры
Автор задачи: Ден Расковалов Источник задачи: Десятый командный чемпионат школьников Свердловской области по программированию (16 октября 2004 года) |
