Учёные, специализирующиеся в области колдовских наук, недавно открыли новую элементарную частицу — магион. Изучая законы, которым подчиняется движение магионов, группа из трёх учёных-магов проводит следующий эксперимент.

Ученые создали в лаборатории однородную положительную ауру. Сила взаимодействия с этой аурой имеет постоянную величину и направлена вертикально вверх. Если бы на магион не действовала никакая другая сила, то под действием ауры он бы двигался с постоянным ускорением (0,0,a).

В точку M₁ = (0,0,0) помещается магион, скорость которого равна нулю. В начальный момент времени первый учёный создаёт в точке O₁ сгусток маны. Магион тут же попадает под действие этого сгустка и, пока тот существует, находится на расстоянии O₁M₁ от точки O₁. В результате магион начинает движение вверх по дуге окружности omega₁ с центром в O₁.

В некоторый момент времени первый учёный испаряет сгусток маны в O₁, а второй учёный одновременно создаёт свой сгусток в точке O₂. Момент для этого выбирается следующим образом.

Расположение точки O₂ выбирается так, чтобы точка M₂ была однозначно определена и не совпадала с точкой M₁. Магион, попав под действие второго сгустка, продолжает своё движение по окружности omega₂ с центром в точке O₂, проходящей через точку M₂.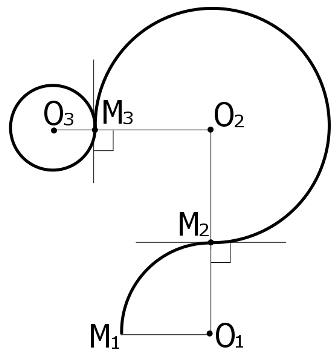

После чего процедура повторяется — второй учёный испаряет свой сгусток маны, а третий учёный создаёт свой в точке O₃. Магион, находящийся в этот момент времени в точке M₃, теперь начинает двигаться по окружности omega₃ с центром в O₃. Третий учёный ждёт, пока магион не опишет полный круг по окружности omega₃ и не вернётся в точку M₃. Этот момент считается моментом завершения эксперимента.

Все учёные выбирают моменты и места создания сгустков маны так, чтобы точка M_i не совпадала с точками M_i−1 и O_i, а расстояние от O_i до любой точки окружности omega_i−1, отличной от точки M_i, было строго больше O_iM_i. Кроме того, учёные следят, чтобы в каждый момент времени, кроме начального, скорость магиона не была равна нулю.

В любой момент времени на магион действуют ровно две силы: сила взаимодействия со сгустком маны и сила взаимодействия с аурой. Первая из них всегда направлена перпендикулярно траектории движения магиона и поэтому не влияет на модуль его скорости.

Сможете ли вы, зная координаты точек O_i и величину ускорения a, определить суммарную длину участков траектории магиона, на которых его скорость была не менее v?

В первой строке записано целое число t — количество экпериментов, проведённых учёными (1 ≤ t ≤ 1000). Далее дано описание экспериментов, каждый эксперимент описывается блоком из четырёх строк.

В первой строке блока записаны целые числа v и a (1 ≤ v ≤ 50 000; 1 ≤ a ≤ 1000). В каждой из следующих трёх строк блока записаны целые числа x_i, y_i, z_i — координаты точки O_i (−10⁶ ≤ x_i, y_i, z_i ≤ 10⁶; x₁² + y₁² > 0). Гарантируется, что в траектории магиона не будет горизонтальной дуги, по которой он будет перемещаться со скоростью v.

Для каждого проведённого эксперимента в отдельной строке выведите суммарную длину участков траектории магиона, на которых его скорость была не менее v. Ответы должны иметь абсолютную или относительную погрешность не более 10⁻⁶.

В данном примере был проведён один эксперимент. Траектория имеет следующий вид:
от точки (0,0,0) до точки (4,0,2) — дуга меры arcsin(0.8) окружности с радиусом 5;
от точки (4,0,2) до точки (20,16,2) — четверть окружности с радиусом 16;
от точки (20,16,2) до точки (20,16,2) — полная окружность с радиусом 1.