| ENG RUS | Timus Online Judge |
Соревнование школьников. Октябрь 2004
Соревнование завершено
B. ФайрболлОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ Все, наверное, знают о научно-исследовательском подразделении Ночного дозора в городе Соловец. В результате хитроумного шага Завулона, это НИИ чародейства и волшебства было полностью рассекречено ещё в 60-е годы. Однако это ничуть не мешает ему работать и по сей день. В частности, прямо сейчас в одном из подразделений НИИ ЧАВО города Соловца некто маг третьего уровня Витька Корнеев испытывает новое заклинание файрболла — это такой огненный шар, использующийся для… м-м-м… нейтрализации нежелательных последствий. Новый файрболл оказался просто гениальным изобретением! Мало того, что его физический радиус (в отличие от видимого), благодаря неконгруэнтности трансгрессии в пси-поле инкуб-преобразования фактически был нулевым. Так он ещё и имел замечательную особенность оставаться устойчивым в течении наперед заданного количества столкновений с различными препятствиями. Такое свойство назвали N-устойчивостью: файрболл является N-устойчивым, если после N столкновений он еще остаётся в стабильном состоянии, а после (N + 1)-го взрывается и аннигилирует. Таким образом можно считать, что после столкновения со стеной файрболл теряет 1 уровень устойчивости, превращаясь из N-устойчивого в (N − 1)-устойчивый файрболл. Для примера, обычный файрболл является 0-устойчивым. Таким образом, стало возможным метать файрболл в цель рикошетом от стены или потолка. Или даже после нескольких рикошетов поразить стоящего к тебе лицом врага файрболлом прямо в спину! В общем, боевые возможности этого нового заклинания были крайне впечатляющие. В добавок ко всему, новый N-устойчивый файрболл при N > 0 ведет себя крайне необычно: Он свободно пролетает сквозь любые препятствия, кроме бетонных стен, от которых отскакивает (теоретики связывают этот эффект с накоплением био-эмоционального заряда, свойственным всем статическим конструкциям достаточно старых жилых помещений). Это, как вы уже, наверное, догадались, порождает ещё более ценные свойства нового изобретения: Например, можно кинуть файрболл себе за спину, после чего файрболл отразится от стены сзади, пройдет сквозь вас и поразит ничего не понимающего противника! Великолепный боевой приём, не правда ли? Но от опытного образца до массового внедрения также как муравью до Луны. Для начала следует исследовать траекторию файрболла при отражениях от стен. Для этого решили провести следующий эксперимент: в прямоугольной комнате, случайно выбирают две точки A и B. Чародей, метающий файрболл, становится в точку A, а мишень помещается в точку B. Чародей создаёт N-устойчивый файрболл, его ассистент с помощью специальной программы рассчитывает направление, в котором файрболл необходимо кинуть, чтобы он, совершив ровно N отскоков от стен, попал прямо в мишень. И при этом сделал это как можно быстрей. После этого чародей запускает файрболл в рассчитанном направлении и проверяет, что он действительно поражает мишень. Собственно вам и предстоит написать эту самую специальную программу, для расчёта направления броска. Теоретики НИИ утверждают, что файрболлы отскакивают от стен по закону «угол падения равен углу отражения» а при попадании точно в угол комнаты файрболл отскакивает точно в обратном направлении. Кроме того, теория говорит, что из соображений непрерывности времени жизни файрболла по направлению броска, соударение с углом комнаты эквивалентно двум соударениям со стенками. То есть 2-устойчивый файрболл, ударившийся один раз точно в угол, аннигилирует при следующем же столкновении. Кроме того, можно считать сам файрболл точкой, двигающейся после броска прямолинейно, с постоянной по модулю скоростью. 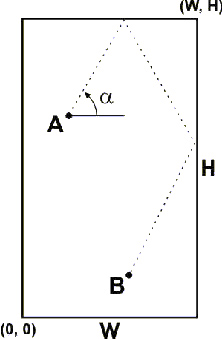 Исходные данныеВ первой строке через пробел находятся два числа — ширина и длина комнаты в метрах. Во второй строке находится число N — N-устойчивость файрболла. В третьей строке находятся ещё четыре числа — координаты точек A и B.
Все числа целые, и разделяются в строке одним или несколькими пробелами. A и B лежат в пределах комнаты и не лежат на её границе, а сама комната не больше 1000 метров в длину и ширину. Ширина и длина комнаты не менее двух метров. На данный момент придумали способ создавать N-устойчивые файрболлы с РезультатУгол в градусах (с точностью до 2 знаков после десятичной точки), задающий направление метания файрболла, чтобы он, сделав ровно N отражений от стен комнаты, попал в точку B, двигаясь при этом по кратчайшей траектории. Если таких углов несколько, вывести нужно минимальный. Угол и координаты отсчитываются, как показано на рисунке. Пример
ЗамечанияПерсонажи и события заимствованы из книг «Понедельник начинается в субботу» (Аркадий и Борис Стругацкие) и тетралогии «Ночной дозор», «Дневной дозор», «Сумеречный дозор» и «Последний дозор» (Сергей Лукьяненко)
Автор задачи: Павел Егоров Источник задачи: Десятый командный чемпионат школьников Свердловской области по программированию (16 октября 2004 года) |
