| ENG RUS | Timus Online Judge |
Dmitry Gozman Contest 1. Petrozavodsk training camp. Winter 2007
Соревнование завершено
J. Zones on a PlaneОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ 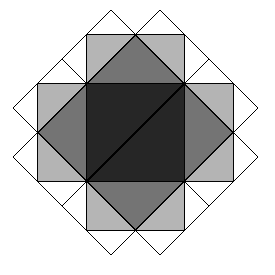 Consider zones zi on a plane which consist of triangles. Zone z1
consists of two right-angled isosceles triangles, forming a square. Zone
zn + 1 is produced from zone zn in the following way. For each
triangle from the previous zone, construct two isosceles right-angled
triangles on each of its two legs as a hypotenuse. Then, remove every
triangle that is a part of a zone with lower number. The remaining triangles
constitute the zone zn + 1.
Given an integer number n, find how many simple polygons constitute
the zone zn.
Исходные данныеThere is a single integer n (1 ≤ n ≤ 2000) on the first line
of the input.
РезультатOutput a single number — the number of simple polygons zone zn
consists of.
Примеры
Автор задачи: Dmitry Gozman Источник задачи: Dmitry Gozman Contest 1, Petrozavodsk training camp, January 2007 |
