| ENG RUS | Timus Online Judge |
Соревнование школьников. Октябрь 2001
Соревнование завершено
A. Кусочно-постоянная функцияОграничение времени: 0.5 секунды Ограничение памяти: 64 МБ 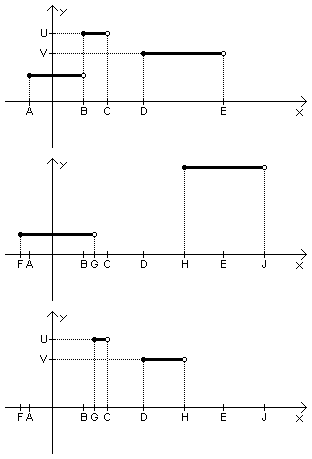 Последние три месяца СКБ Контур ведёт разработку принципиально новой инструментальной среды SKB Kontur Framework. Одной из новинок будет представление некоторых данных в виде кусочно-постоянных функций. Вашей команде предстоит реализовать операцию наложения двух таких функций. Кусочно-постоянной функцией называется функция, область определения которой разбивается на интервалы, на каждом из которых функция постоянна. Будем также считать, что на левой границе интервала постоянности значение функции совпадает с её значением на всём интервале. На рис.1 приведена кусочно-постоянная функция с тремя интервалами постоянности. Заметим, что в точке B значение функции есть U, а в точках C и E, и на интервале (C;D) значение функции не определено. Наложением двух кусочно-постоянных функций F1 @ F2 назовём кусочно-постоянную функцию F такую, что:
На рис.3 приведено наложение функции на рис.1 на функцию на рис.2. Исходные данныеВвод состоит из двух строк одинакового формата. Каждая строка описывает одну кусочно-постоянную функцию. Строка начинается с целого числа N (1 ≤ N ≤ 15000). Далее следуют описания N интервалов постоянности, упорядоченные по возрастанию левой границы. Каждый интервал задаётся тройкой целых чисел A, B, Y (|A| < 32000, |B| < 32000, |Y| ≤ 100, A < B), где A — левая граница интервала, B - правая граница интервала, Y — значение функции на этом интервале. Известно, что никакая пара интервалов из одной строки не пересекается, и нет двух смежных интервалов, на которых значения функции совпадают. РезультатВывод состоит из одной строки в том же формате, что и ввод. Эта строка должна описывать наложение кусочно-постоянных функций, описанных в первой и во второй строках ввода. Пример
Автор задачи: Олег Кац Источник задачи: USU Open Collegiate Programming Contest October'2001 Junior Session |
